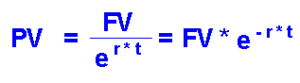Present Value of Single Cash Flow for Multiple Periods with Continuous Compound Interest
Present Value with a Single Cash Flow:
Present value (PV) is the current value of a single future cash flow discounted at the appropriate discount rate.
Time value of money for a single cash flow is a cash inflow or outflow that investors or lenders received from or paid to once respectively for specific periods
There are often four parts to equation (time value of money for a single cash flow): the present value (PV), the future value (FV), the discount rate (r), and the number of periods of the investment (t). If three of these (FV, r and t) are given, so we can find the present value (PV).
Multiple-Period Investment:
Multiple-period investment may be investment for more than one year. Term multiple-period can refer to more than one day or one month investment, so it isn’t always more than one year investment.
If period investments are based on one day, one month or one year etc., so discount rates are based on one day, one month or one year respectively.
Definition of Continuous Compound Interest:
We could compound semiannually, quarterly, monthly, daily, hourly, each minute, or even more often by using PV=FV/(1+r/m)mt, but when it is compounded discount rate continuously, so we cannot use this formula.
Formula of Future Value with Continuous Compound Interest for Multiple-Period Investment:
FV=PV*ert
so
which
e : is a constant , and e≈2.7182
PV: Present Value or principal is worth today
FV: Future value is worth in the future
r : Interest rate, rate of return, or discount rate per period , but not always one year.
t : time is referred to number of periods of investment
Question
Your company is going to pay you $1,000 at the end of four years when you leave job. If the continuously compounded rate of interest is 8 percent, what is the present value of this payment?
Solution
PV=FVe^(-rt)=1,000*e^(-0.08*4)=1,000*0.7261=$726.1
So present value of this payment is only 726.1