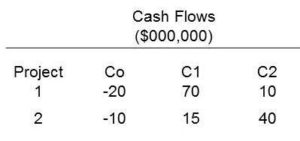
Net Present Value (NPV) for Mutually Exclusive Project
Mutually exclusive project is different independent project. For mutually exclusive project, we can accept project A or B or deny both, but we cannot accept both projects.
We may solve mutually exclusive projects using NPV with following two methods:
- Compare NPV if NPV(A)>NPV(B), so choose project A
- Compute incremental NPV solved via cash flows from project A minus project B, and if incremental NPV > O, so choose project A.
Note: Please note that NPV(A) and NPV(B) are positive values.
Example:
ABC Corporation applies a 12 percent discount rate to two investment opportunities, and we assume both projects are mutually exclusive projects.
Required:
- Determine NPVs for both projects.
- Determine incremental NPV, you may subtract project 1 cash flows from project 2 cash flows to solve incremental NPV.
- Make decision for these projects.
Solution:
- NPVs
NPV (project 1) = 70/(1+12%)^1 + 10/(1+12%)^2 – 20 =$ 50,500,000
NPV (project 2) = 15/(1+12%)^1 + 40/(1+12%)^2 – 20 =$ 35,300,000
- Incremental NPV
Subtracting project 1 cash flows from project 2 cash flows gives the following results:
Cash flow (Year 0) =-20-(-10)=-10
Cash flow (Year 1)= 70 -15 =55
Cash flow (Year 2) =10-40=-30
Incremental NPV (project 1- project 2) = 55/(1+12%)^1-30/(1+12%)^2 – 10 = $15,200,000
- Decision
We can make decisions with following two methods using NPV giving the same answer.
- Method 1, we compare NPVs
NPV (project 1) > NPV (project 2) or $50,500,000 > $35,300,000
Because both projects are mutually exclusive projects, so we cannot choose both projects although
they have both positive NPVs. Project 1 is chosen.
- Method 2, incremental NPV
Incremental NPV (project 1- project 2) = $15,200,000 > 0
Because incremental NPV ( project 1 – project 2) are positive and both projects are mutually exclusive projects, so Project 1 is chosen.
Source:
- Phnom Penh HR
- Mcgraw-Hill – Fundamentals Of Corporate Finance