Net Present Value (NPV) for Capital Rationing

Net Present Value (NPV) for Capital Rationing 

In real situations, company may not have enough capitals to invest all profitable projects, so we need to choose projects that give optimal profit and meet with our capitals that have.

Project Decision:

Combined possible NPVs with available capitals and compare combined NPVs.

For example, Combined NPVs (case 1) > Combined NPVs (case2), so we will choose Case 1.

Example:

ABC Corporation applies a 12 percent discount rate to three investment opportunities, and these projects provide profitable and positive NPVs, but ABC Corporation cannot afford all projects because of insufficient capitals.

 

Required:

1. Make decision, we assume that company has $20 million to invest projects.
2. Make decision, we assume that company has $30 million to invest projects.

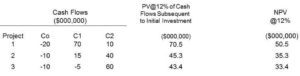
1. $20 million capital

• Project 1 : Capital = $20 million, NPV = $50.5 million
• Project 2 : Capital = $10 million, NPV = $35.3 million
• Project 3 : Capital = $10 million, NPV = $33.4 million

Possible Combined NPVs with available capital of $20 million as follows:

• Combined NPV (project 2 and 3) = $35.3 + $33.4 = $68.7 million, and Combined Capitals = $10 + $10 = $20 million
• NPV (project 1) =$50.5 million, and capital=$20 million

This case assumes firm has only $ 20 million to invest, so firm cannot chose all projects that have positive NPV. What should the firm do? Firm should choose either project 1 (capital of $20 million) or projects 2 and 3 (capital=$10 million + $10 million=$20 million). Individually, projects 2 and 3 have lower NPVs than project 1 has. However, when the NPVs of projects 2 and 3 are added together, the sum is higher than the NPV of project 1. Thus, common sense dictates that projects 2 and 3 shall be accepted.

2. $30 million capital

• Project 1 : Capital = $20 million, NPV = $50.5 million
• Project 2 : Capital = $10 million, NPV = $35.3 million
• Project 3 : Capital = $10 million, NPV = $33.4 million

Possible Combined NPVs with available capital of $20 million as follows:

• Combined NPV (project 1 and 2) = $50.5 + $35.3 = $85.8 million, and Combined Capitals = $20 + $10 = $30 million
• Combined NPV (project 1 and 3) = $50.5 + $33.4 = $83.9 million, and Combined Capitals = $20 + $10 = $30 million
• Combined NPV (project 2 and 3) = $35.3 + $33.4 = $68.7 million, and Combined Capitals = $10 + $10 = $20 million

This case assumes firm has $30 million to invest, so firm should accept projects 1 and 2 because the sum of the NPVs of these projects is greater than the sum of the NPVs of projects 2 and 3 or NPVs of projects 1 and 3.

Projects 2 and 3 have a combined initial investment of only $20 million (10+10). If the projects 2 and 3 are accepted, the remaining $10 million must be left in the bank.

Source:

1. Phnom Penh HR
2. Mcgraw-Hill – Fundamentals Of Corporate Finance