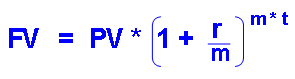Future Value of Single Cash Flow for Multiple-Period Investment with Frequency Compound Interest

Future Value of Single Cash Flow for Multiple-Period Investment with Frequency Compound Interest

Future Value with a Single Cash Flow:

Time value of money for a single cash flow is a cash inflow or outflow that investors or lenders received from or paid to once respectively for specific periods.

Future value (FV) refers to the amount of money an investment or present value (PV) will grow for specific periods of time at specific interest rate.

Future Value = Present Value + all earned interests

Multiple-Period Investment:

Multiple-period investment may be investment for more than one year. Term multiple-period can refer to more than one day or one month investment, so it isn’t always more than one year investment.

If period investments are based on one day, one month or one year etc., so discount rates are based on one day, one month or one year respectively.

Definition of Frequency Compound Interest:

The compounding frequency is the number of times per year the accumulated interest is paid out on a regular basis. The frequency could be yearly, half-yearly, quarterly, monthly, weekly, daily etc.

Formula of Future Value with Compounding Frequency for Multiple-Period Investment:

Which

PV: Present Value or principal is worth today

FV: Future value is worth in the future

r : Interest rate, rate of return, or discount rate per period , but not always one year.

t : time is referred to number of years (but not always year) of investment

m: Compounding Frequency:

• If compound yearly, then m=1
• If compound semiannually, then m=2
• If compound quarterly, then m=4
• If compound monthly, then m=12
• If compound daily, then m=365

r/m: it is called rate per compounding period (i), so let i =r/m

m x t: it is called numbers of periods in t years, so let N= m x t

 Question 1

AAB Royal Company is investing $5,000 at bank with annual interest rate of 8 percent per year, compounded quarterly, for five years.

What is his wealth at the end of five years?

Solution

FV=PV x (1+r/m)^m*t

FV=$5,000 x (1+8%/4) ^(4*5)=$7,430

So his wealth at the end of five years = $7,430

Question 2

You deposited of $2,000 in an account that bank pays interest at a rate of 10% per year.

We assume that interest compounded for different compounding frequencies as follows:

• Annual
• Semiannual
• Quarterly
• Monthly

How much is in the account after, say, three years depends on the compounding frequency?

Solution

We use formula, FV=PV x (1+r/m) ^m*t

which

i=r/m

N= m x t

t=3

Compounding Frequency	m	r	PV	N	i	FV at the End of Three Years
Annual	1	10%	$2,000	3	10%	$2,662
Semiannual	2	10%	$2,000	6	5%	$2,680
Quarterly	4	10%	$2,000	12	3%	$2,690
Monthly	12	10%	$2,000	36	1%	$2,696

Please note that more compounding frequency, the more future value worth we get.